Вступление
В этом сообщении будут рассмотрены две темы: одна из сферы машинного обучения и программирования на R, а вторая - из области разработки лекарственных средств.Существует особая процедура регистрации генерических лекарственных препаратов - так называемый биовейвер. В этом случае при оценке биоэквивалентности вместо сравнительных фармакокинетических/фармакодинамических/клинических испытаний (in vivo) проводятся тесты на растворимость и проникаемость (in vitro). В качестве стандартной модели для оценки проникаемости веществ используется монослой клеток линии Caco2, и актуальной задачей является прогнозирование степени проникаемости (по сути - скорости пассивной диффузии) исходя из известных свойств изучаемого вещества, чтобы не ставить лишние эксперименты для веществ с плохой проникаемостью.
Анализируемые данные
Озвученной выше проблеме посвящена работа ADME evaluation in drug discovery. 5. Correlation of Caco-2 permeation with simple molecular properties. В ней приводится таблица, содержащая характеристики 77 различных по структуре веществ, а также экспериментальные данные по проникаемости этих веществ. Следует отметить, что данные, полученные для одного и того же вещества в ходе разных экспериментов, могут значительно варьировать. Но мы не будем углубляться в этот аспект проблемы, а просто возьмем те данные, с которыми работали авторы публикации.df <- read_excel("caco2.xlsx")
glimpse(df)## Observations: 77
## Variables: 10
## $ name <chr> "acebutolol", "acebutolol_ester", "acetylsalic_...
## $ log_P_eff_exp <dbl> -5.83, -4.61, -5.06, -6.15, -4.62, -4.47, -4.44...
## $ log_D <dbl> -0.09, 1.59, -2.25, -1.80, 1.38, 2.78, 0.63, 2....
## $ rgyr <dbl> 4.64, 5.12, 3.41, 3.37, 3.68, 3.84, 2.97, 2.75,...
## $ rgyr_d <dbl> 4.51, 5.03, 3.24, 3.23, 3.69, 3.88, 2.97, 2.75,...
## $ HCPSA <dbl> 82.88, 77.08, 79.38, 120.63, 38.92, 35.53, 20.8...
## $ TPSA <dbl> 87.66, 93.73, 89.90, 114.76, 41.49, 47.56, 26.7...
## $ N_rotb <dbl> 0.31, 0.29, 0.23, 0.21, 0.29, 0.27, 0.17, 0.07,...
## $ log_P_eff_calc <dbl> -5.30, -4.89, -5.77, -5.91, -4.58, -4.39, -4.63...
## $ residuals <dbl> -0.53, 0.28, 0.71, -0.24, -0.04, -0.08, 0.19, -...log_P_eff_exp - логарифм скорости диффузии (которая измеряется в см/с).Список предикторов:
- log_D - коэффициент распределения при pH = 7.4;
- rgyr - радиус гирации;
- rgyr_d - динамический радиус гирации;
- HCPSA - площадь сильно заряженной полярной поверхности;
- TPSA - топологическая площать полярной поверхности;
- N_rotb - число поворотных связей.
ggpairs(df,
columns = c(3:8),
diag = list(continuous = "barDiag"))Переменные
rgyr и rgyr_d, а также HCPSA и TPSA предсказуемо сильно коррелируют, поскольку в обоих случаях пары переменных представляют собой разные способы расчета одной и той же физической величины.Для графического анализа взаимосвязей предикторов и целевой переменной переформатируем данные в “длинный” формат:
df_long <- df %>%
gather(vars, values, -c(name, log_P_eff_exp, log_P_eff_calc, residuals))ggplot(df_long) +
geom_point(aes(x = values,
y = log_P_eff_exp)) +
facet_wrap(~ vars,
scales = "free")Мы видим, что существуют как положительные, так и отрицательные корреляции предикторов с целевой переменной, но они относительно слабо выражены, и по графикам тяжело определить, какая форма нелинейной взаимосвязи может иметь место.
Кстати, корреляции между переменными удобно анализировать при помощи пакета corrr:
x <- correlate(df[, 2:8])
network_plot(x, legend = TRUE)Попробуем подойти к проблеме как к классической задаче машинного обучения: проверим несколько моделей разных классов и выберем из них оптимальную с точки зрения качества на отложенной выборке. Поскольку набор данных чрезвычайно мал, в качестве стратегии перекрестной проверки выберем скользящий контроль по отдельным объектам (leave-one-out CV).
Средний квадрат остатков (MSE) для подобранной авторам модели равен 0.1876. С этим значением будем сравнивать полученные далее результаты.
Машинное обучение с использованием пакета pipelearner
Пакет pipelearner представляет собой легковесную альтернативу таким библиотекам, как caret или mlr. В основе - tidyverse, “аккуратные данные” и конвейерный оператор %>%. Пакет хорошо документирован, все непонятные моменты можно прояснить, просто изучив структуру объекта с моделями на каждом этапе.В качестве базовой модели построим простую линейную модель:
df <- df %>%
select(-c(name, log_P_eff_calc, residuals))
results <- df %>%
pipelearner() %>%
learn_cvpairs(k = nrow(df)) %>% # для реализации leave-one-out
learn_models(lm, log_P_eff_exp ~ .) %>%
learn()
results## # A tibble: 77 x 9
## models.id cv_pairs.id train_p fit target model params
## <chr> <chr> <dbl> <list> <chr> <chr> <list>
## 1 1 01 1 <S3: lm> log_P_eff_exp lm <list [1]>
## 2 1 02 1 <S3: lm> log_P_eff_exp lm <list [1]>
## 3 1 03 1 <S3: lm> log_P_eff_exp lm <list [1]>
## 4 1 04 1 <S3: lm> log_P_eff_exp lm <list [1]>
## 5 1 05 1 <S3: lm> log_P_eff_exp lm <list [1]>
## 6 1 06 1 <S3: lm> log_P_eff_exp lm <list [1]>
## 7 1 07 1 <S3: lm> log_P_eff_exp lm <list [1]>
## 8 1 08 1 <S3: lm> log_P_eff_exp lm <list [1]>
## 9 1 09 1 <S3: lm> log_P_eff_exp lm <list [1]>
## 10 1 10 1 <S3: lm> log_P_eff_exp lm <list [1]>
## # ... with 67 more rows, and 2 more variables: train <list>, test <list>results <- results %>%
mutate(true = map2_dbl(test, target, ~as.data.frame(.x)[[.y]]),
predicted = map2_dbl(fit, test, predict))
ggplot(results, aes(true, predicted)) +
geom_point(size = 2) +
geom_abline(intercept = 0, slope = 1, linetype = 2) +
labs(x = "Истинное значение", y = "Предсказанное значение") +
xlim(-7, -4) +
ylim(-7, -4) +
coord_fixed()Видим, что модель систематически завышает маленькие значения и занижает большие.
Рассчитаем MSE:
summarise(results,
MSE = mean((predicted - true)^2))## # A tibble: 1 x 1
## MSE
## <dbl>
## 1 0.2356067\[\min_{\beta_0,\beta} \frac{1}{N} \sum_{i=1}^{N} w_i l(y_i,\beta_0+\beta^T x_i) + \lambda\left[(1-\alpha)||\beta||_2^2/2 + \alpha ||\beta||_1\right]\]
Дополнительный штраф представляет собой сумму l1-нормы и l2-нормы вектора коэффициентов модели в некоторой пропорции, которая задается величиной \(\alpha\), умноженную на константу \(\lambda\). Соответственно, нужно предварительно нормировать переменные:
# df_norm <- df %>%
# dmap(~ (.x - mean(.x)) / sd(.x))
# df_norm$log_P_eff_exp <- df$log_P_eff_exp
df_norm <- df %>%
mutate_each(funs((. - mean(.)) / sd(.)), -log_P_eff_exp)x и y), нужно написать вспомогательную функцию, аналогичную этой:glmnet_formula <- function(data, formula, ...) {
data <- as.data.frame(data)
X_names <- as.character(lazyeval::f_rhs(formula))
y_name <- as.character(lazyeval::f_lhs(formula))
if (X_names == '.') {
X_names <- names(data)[names(data) != y_name]
}
X <- data.matrix(data[, X_names])
y <- data[[y_name]]
glmnet(x = X, y = y, ...)
}alpha = c(0.1, 0.5, 1), lambda = c(0, 0.05, 0.15).results <- df_norm %>%
pipelearner() %>%
learn_cvpairs(k = nrow(df_norm)) %>% # для реализации leave-one-out
learn_models(glmnet_formula,
log_P_eff_exp ~ .,
family = "gaussian",
alpha = c(0.1, 0.5, 1),
lambda = c(0, 0.05, 0.15)) %>%
learn()predict.glmnet(). Также добавляем столбец-индикатор гиперпараметров моделей:results <- results %>%
mutate(true = map2_dbl(test, target, ~as.data.frame(.x)[[.y]]),
predicted = map2_dbl(fit, test,
function(.x, .y) {
# убираем целевую переменную
tmp <- as.data.frame(.y)[, -1]
class(tmp) <- "data.frame"
tmp <- data.matrix(tmp)
predict(object = .x, newx = tmp)
}
),
MSE = (predicted - true) ^ 2, # для одного наблюдения
model_hparams = map_chr(params,
~ paste0("alpha_",
.x$alpha,
"_",
"lambda_",
.x$lambda))
)ggplot(results, aes(model_hparams, MSE)) +
# geom_jitter(width = .03, alpha = .3) +
geom_boxplot() +
stat_summary(geom = "point", fun.y = mean, size = 4) +
theme(axis.text.x = element_text(angle = 90, hjust = 1))Как видим, улучшить результаты простой линейной модели (на графике ей соответствует первый боксплот) практически не удалось. При этом для большинства наблюдений ошибка невелика, зато для нескольких наблюдений она очень большая.
Для сравнения попробуем построить несколько решающих деревьев:
results <- df %>%
pipelearner() %>%
learn_cvpairs(k = nrow(df)) %>% # для реализации leave-one-out
learn_models(rpart,
log_P_eff_exp ~ .,
minsplit = c(2, 3, 4, 5),
cp = c(0.01, 0.05)) %>%
learn()
results <- results %>%
mutate(true = map2_dbl(test, target, ~as.data.frame(.x)[[.y]]),
predicted = map2_dbl(fit, test, predict),
MSE = (predicted - true) ^ 2, # для одного наблюдения
model_hparams = map_chr(params,
~ paste0("minsplit_",
.x$minsplit,
"_",
"cp_",
.x$cp))
)
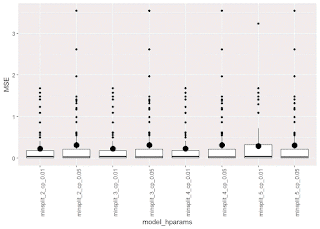
ggplot(results, aes(model_hparams, MSE)) +
# geom_jitter(width = .03, alpha = .3) +
geom_boxplot() +
stat_summary(geom = "point", fun.y = mean, size = 4) +
theme(axis.text.x = element_text(angle = 90, hjust = 1))Результаты примерно такие же; в качестве оптимальной можно выбрать модель с
minsplit = 2 и cp = 0.01. В целом можно сделать выводы, что для большинства веществ можно предсказать степень проникаемости с достаточно высокой точностью, то есть подобные модели целесообразно использовать при планировании реальных экспериментов.




Комментариев нет:
Отправить комментарий